前言

深度优先遍历（Depth First Search, 简称 DFS）与广度优先遍历（Breath First Search）是图论中两种非常重要的算法，生产上广泛用于拓扑排序，也频繁出现在 leetcode，高频面试题中。

DFS介绍

深度优先遍历主要思路是从图中一个未访问的顶点V开始，沿着一条路走到底，然后从这条路的尽头的节点回退到上一个节点，再从另一条路开始走到底，以此往复，直到所有的顶点都遍历完成,特点是 不撞南墙不回头先走完一条路再走另一条路。
树是图的特例，我们以DFS来遍历树来加深理解

上图展现了DFS搜索的顺序，那么深度优先遍历该怎么实现呢，有递归和非递归有两种
先看看递归方式

递归

递归三部曲

函数入参和返回值
递归终止条件
单层底层处理逻辑

模板如下

public 参数1 DFS(参数2)
 {
     if(返回条件成立) return 参数 ；
     DFS(进行下一步的搜索遍历) ；
 }

翻译成代码如下

fun dfs(root: TreeNode?, list: MutableList<Int>) {
    if (root == null) return
    //处理节点
    process(root)
    dfs(root.left,list)
    dfs(root.right,list)
}

递归的表达性很好，也比较容易理解，调用类似一个方向盘，有时候在递归中还需要记录性的参数，来标记每条岔路的信息，以便回溯 经典的如岛屿问题

1为陆地，0为水，陆地的左右上下都为0时，为一个岛，假定给定二维数组之外都是0（都是水），问给定一个二维数组确定有几个岛？

这是一个DFS结合数组的经典例子，我们应用DFS将1相连的陆地遍历一遍，这里就需要在DFS的同时记录信息
DFS代码如下

public void dfs(int i , int j ,char[][] grid) //grid为输入的二维数组，i，j为扫描的位置
{
    if(i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] != '1') //“撞南墙”
        return ;
    grid[i][j] = '0' ; //记录节点轨迹，这里的记录方法非常巧妙，将访问之后的陆地变成水，下次自然不会再去访问了
    dfs(i+1,j,grid); //递归调用，来控制访问的方向：左右上下
    dfs(i-1,j,grid);
    dfs(i,j+1,grid);
    dfs(i,j-1,grid);
}

所以在“主函数”中只需找到为“1”的陆地，然后调用DFS让它变成一片海，记录下来调用的次数便是有几个岛屿了
完整代码如下

class Solution {
    public int numIslands(char[][] grid) {
        int res = 0 ;
        for(int i = 0 ; i < grid.length ; i ++)
        {
            for(int j = 0 ; j < grid[0].length ; j++)
            {
                if(grid[i][j] == '1') //找到为1的陆地，调用DFS使之变成大海
                {
                    res ++ ; //记录调用的次数
                    dfs(i,j,grid) ;
                }
            }
        }
        return res ;
    }
    public void dfs(int i , int j ,char[][] grid)
    {
        if(i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] != '1')
            return ;
        grid[i][j] = '0' ;
        dfs(i+1,j,grid);
        dfs(i-1,j,grid);
        dfs(i,j+1,grid);
        dfs(i,j-1,grid);
    }
}

但是如果层级过深的话容易导致栈溢出，这时候就需要考虑非递归实现了

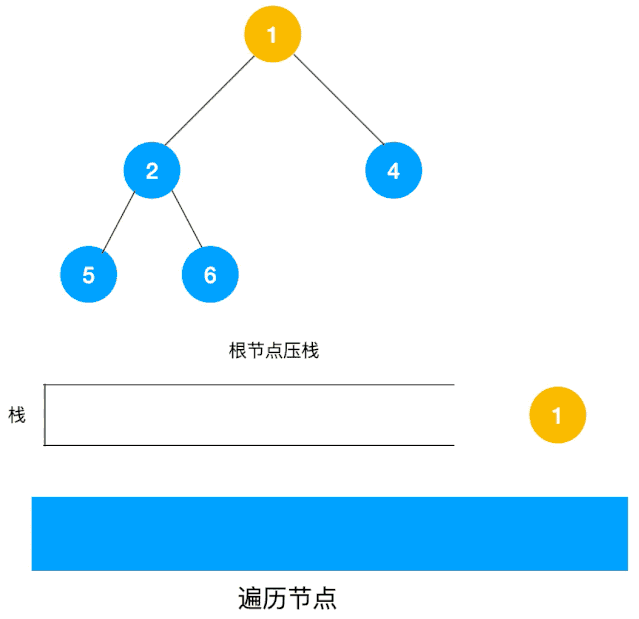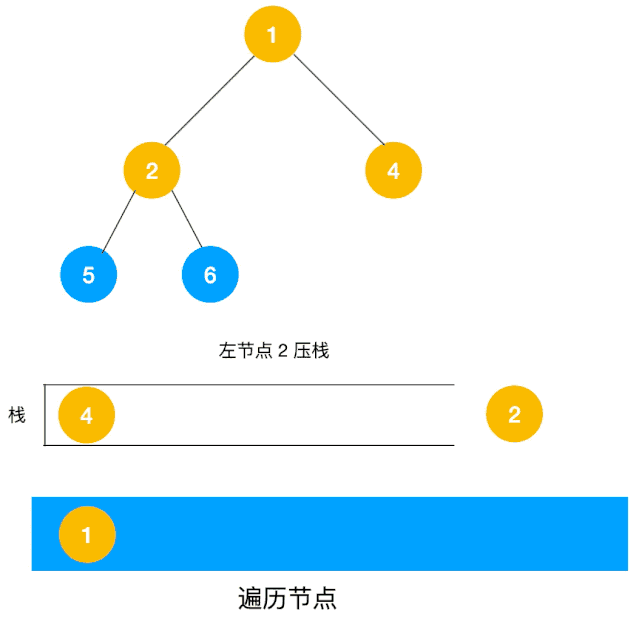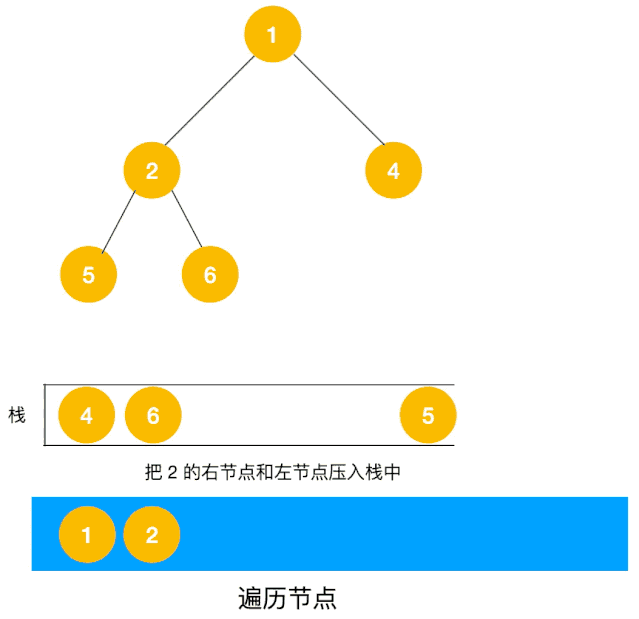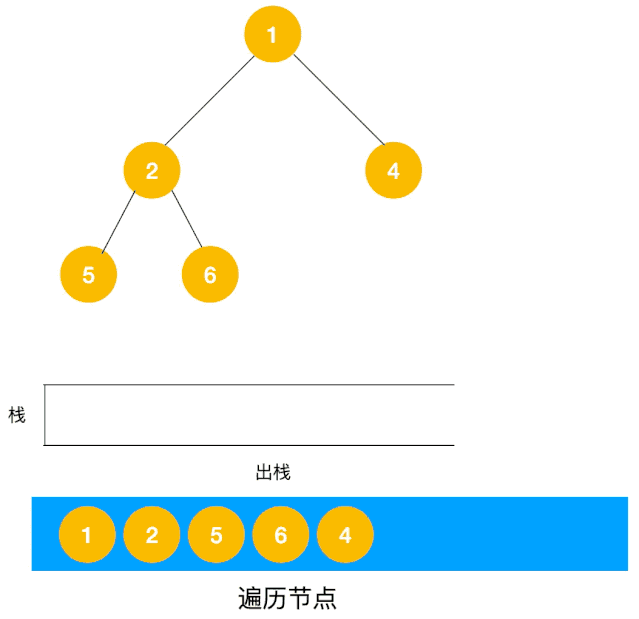
非递归

以二叉树前序(中左右)遍历来看，我们有以下思路

对于每个节点来说，先遍历当前节点，然后把右节点压栈，再压左节点(这样弹栈的时候会拿到左节点遍历，符合深度优先遍历要求)
弹栈，拿到栈顶的节点，如果节点不为空，重复步骤1，如果为空，结束遍历

整体动态如下

可以看到这里借助了栈的数据结构，使用栈来将要遍历的节点压栈，然后出栈后检查此节点是否还有未遍历的节点，有的话压栈，没有的话不断回溯（出栈），有了思路，不难写出如下用栈实现的二叉树的深度优先遍历代码，也不用担心递归那样层级过深导致的栈溢出问题

   //前序遍历迭代法
fun preorderTraversal2(root: TreeNode?): List<Int> {
    val list = mutableListOf<Int>()
    val stack = Stack<TreeNode>()
    if(root == null) return list
    stack.push(root)
    while(!stack.isEmpty()){
        //获取节点
        val node = stack.pop()
        list.add(node.`val`)
        //栈先右后左
        if(node.right!=null) stack.push(node.right)
        if(node.left!=null) stack.push(node.left)
    }
    return list
}

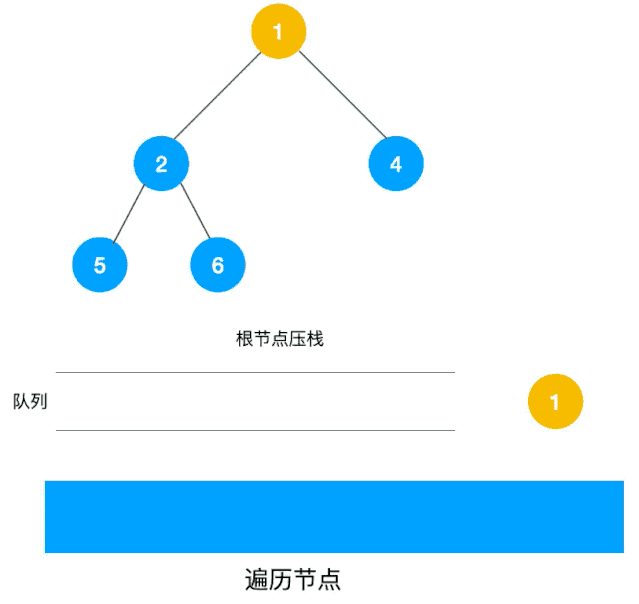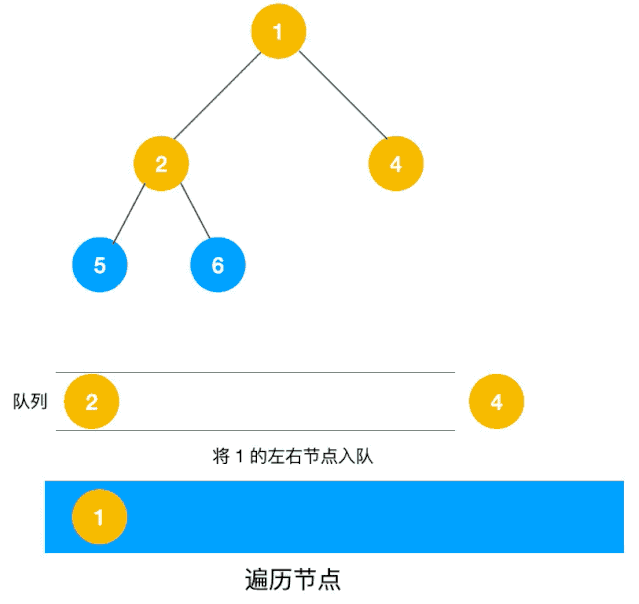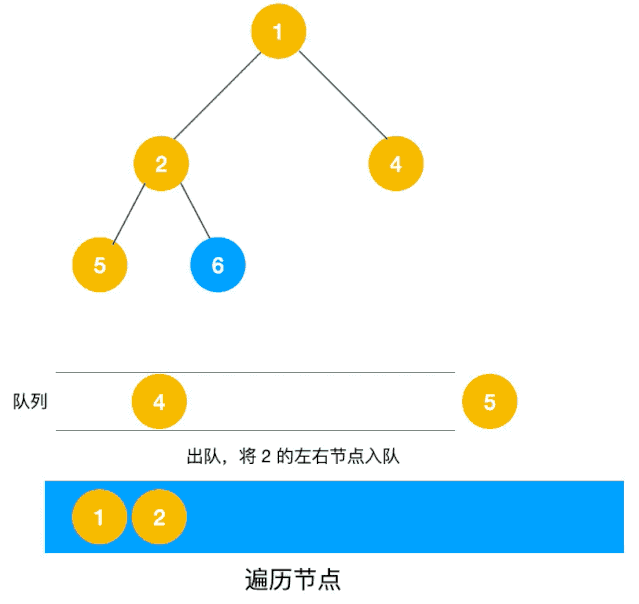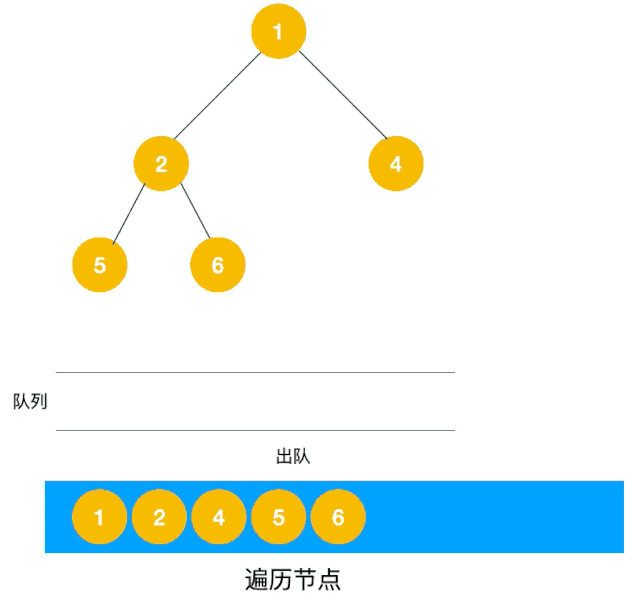
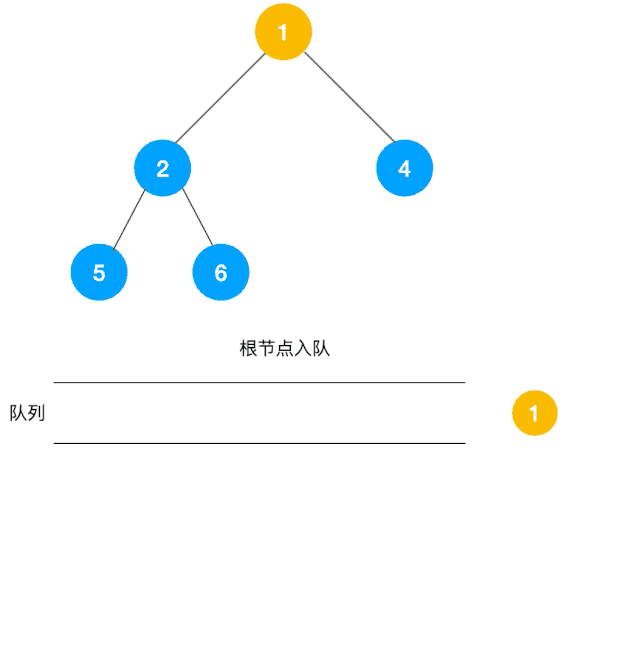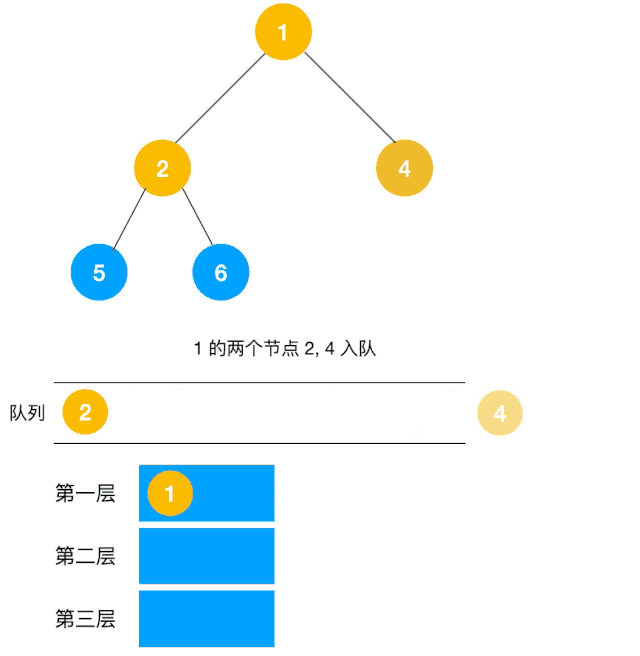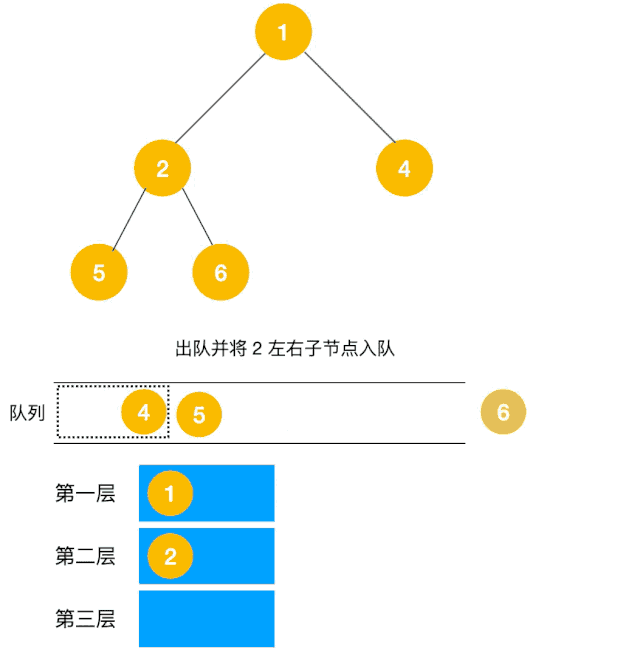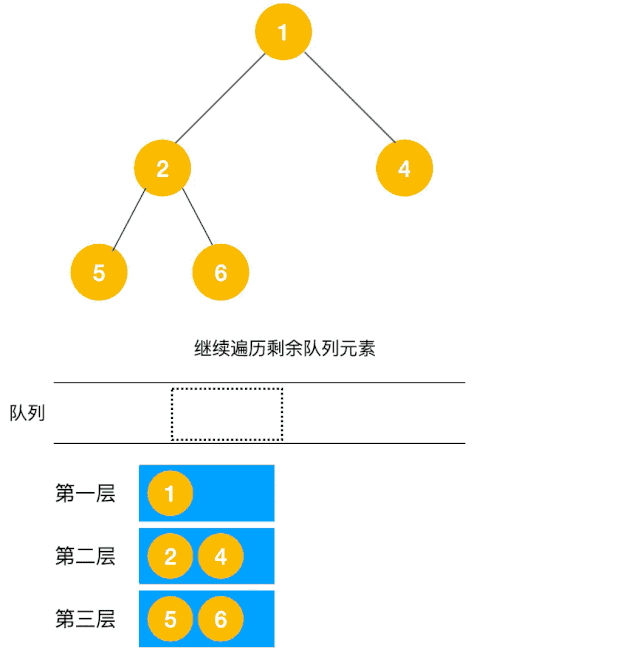
BFS介绍

上面介绍了DFS，重点是依赖于堆栈/递归，较为简单的解决了如何遍历所有元素，但是DFS虽然可以查找到到达路径，但是却找不到最短的路径，针对这一问题，BFS就登场了。
广度优先遍历，指的是从图的一个未遍历的节点出发，先遍历这个节点的相邻节点，再依次遍历每个相邻节点的相邻节点，如下图所示

深度优先搜索使用的是栈，广度优先遍历则是使用队列来实现，我们以二叉树层次遍历为例来看使用广度优先遍历来实现，如下图所示

整体由2层循环组成，外层循环查看队列是否为空(为空元素表示已经遍历完毕)，内层循环用于对当前节点的遍历，以及加入新的节点，内层循环代表一层遍历一层剥洋葱皮 代码如下

fun levelOrder(root: TreeNode?): List<List<Int>> {
    val result = mutableListOf<List<Int>>()
    if (root == null) return result
    val queue = LinkedList<TreeNode>()
    queue.push(root)
    //while循环控制从上到下
    while (!queue.isEmpty()) {
        val size = queue.size
        //记录这一层的节点值
        val curList = LinkedList<Int>()
        for (i in 0..size) {
            val curNode = queue.pop()
            curList.add(curNode.`val`)
            if (curNode.left != null) queue.push(curNode.left)
            if (curNode.right != null) queue.push(curNode.right)
        }
        result.add(curList)
    }
    return result
}

经典题目

Leetcode上一些常使用BFS和DFS来解题的题目

leetcode 104，111: 给定一个二叉树，找出其最大/最小深度。

/**
 * leetcode 104: 求树的最大深度
 * @param node
 * @return
 */
public static int getMaxDepth(Node node) {
    if (node == null) {
        return 0;
    }
    int leftDepth = getMaxDepth(node.left) + 1;
    int rightDepth = getMaxDepth(node.right) + 1;
    return Math.max(leftDepth, rightDepth);
}

/**
 * leetcode 111: 求树的最小深度
 * @param node
 * @return
 */
public static int getMinDepth(Node node) {
    if (node == null) {
        return 0;
    }
    int leftDepth = getMinDepth(node.left) + 1;
    int rightDepth = getMinDepth(node.right) + 1;
    return Math.min(leftDepth, rightDepth);
}

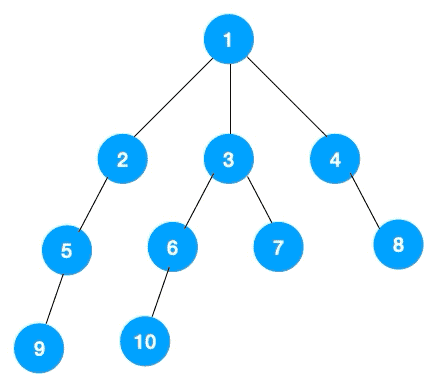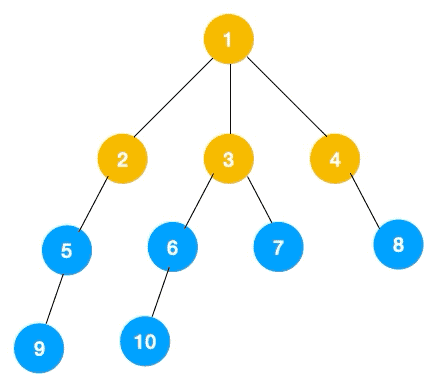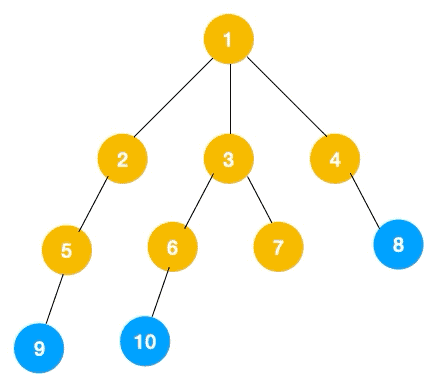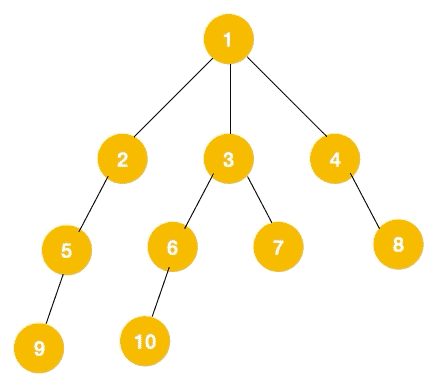
leetcode 102: 给你一个二叉树，请你返回其按层序遍历得到的节点值。（即逐层地，从左到右访问所有节点）。示例，给定二叉树：[3,9,20,null,null,15,7]

这题是BFS的变种，在广度优先遍历过程中，把每一层的节点都添加到同一数组中即可，因此必须事先计算出同一层的节点个数(即队列已有元素)如下图所示

/**
 * leetcdoe 102: 二叉树的层序遍历, 使用 bfs
 * @param root
 */
private static List<List<Integer>> bfsWithBinaryTreeLevelOrderTraversal(Node root) {
    if (root == null) {
        // 根节点为空，说明二叉树不存在，直接返回空数组
        return Arrays.asList();
    }

    // 最终的层序遍历结果
    List<List<Integer>> result = new ArrayList<>();

    Queue<Node> queue = new LinkedList<>();
    queue.offer(root);

    while (!queue.isEmpty()) {
        // 记录每一层
        List<Integer> level = new ArrayList<>();
        int levelNum = queue.size();
        // 遍历当前层的节点
        for (int i = 0; i < levelNum; i++) {
            Node node = queue.poll();
            // 队首节点的左右子节点入队,由于 levelNum 是在入队前算的，所以入队的左右节点并不会在当前层被遍历到
            if (node.left != null) {
                queue.add(node.left);
            }
            if (node.right != null) {
                queue.add(node.right);
            }
            level.add(node.value);
        }
        result.add(level);
    }

    return result;
}