前言

双指针技巧在算法题中算是常用技巧了，让我们省去for循环，降低复杂度，通常双指针技巧可以分为2大类

  • 快慢指针
  • 左右指针

前者主要解决链表中的问题，比如链表是否有环，删除倒数第N个节点等，后者主要解决数组、字符串中的问题，比如二分查找、翻转数组等，下面将详细介绍下

快慢指针

下面结合实例来介绍快慢指针在实际中的用途

判断链表是否有环

单链表的特点是每个节点只知道下一个节点，所以一个指针的话无法判断链表中是否含有环的。如果链表中不含环，那么这个指针最终会遇到空指针 null 表示链表到头了，这还好说，可以判断该链表不含环，如果链表含有环，那么单独一个指针就会陷入死循环。
这时候双指针的作用就体现了，我们使用2个指针，一个跑的快，一个跑的慢。如果没有环的话，跑得快的会遇到null，如果有环的话，快指针最终会和慢指针相遇

1
2
3
4
5
6
7
8
9
10
boolean hasCycle(ListNode head) {
    ListNode fast, slow;
    fast = slow = head;
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
        if (fast == slow) return true;
    }
    return false;
}

链表是否有环，有的话返回这个环的起始位置

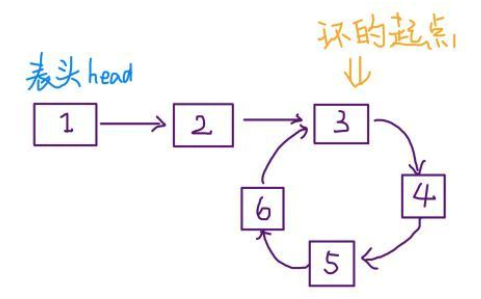
image.png
这个题目多了一些数学计算

  1. 先找相遇点 判断是否有环
  2. 有环的话重置其中一个指针到起点，相同速度前进，再次相遇就是节点位置开始的位置
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    public ListNode detectCycle(ListNode head) {
        ListNode slow,fast;
        slow = fast = head;
        boolean hasRecycle = false;
        //快慢指针找到交点
        while(fast!=null && fast.next!=null){
            slow = slow.next;
            fast = fast.next.next;
            if(slow == fast) {
                hasRecycle = true;
                break;
            }
        }   
        if(!hasRecycle) {
            return null;
        }
        
        //将其中一个重置到起点,再一起移动，下次相交就是相遇点
        slow = head;
        //int index = 0;
        while(slow!=fast){
            slow = slow.next;
            fast = fast.next;
            //index++;
            if(slow == fast) break;
        }
        return slow;
    }

    解释下原理
    可以看到，当快慢指针相遇时，让其中任一个指针指向头节点，然后让它俩以相同速度前进，再次相遇时所在的节点位置就是环开始的位置。这是为什么呢？

第一次相遇时，假设慢指针 slow 走了 k 步，那么快指针 fast 一定走了 2k 步，也就是说比 slow 多走了 k 步（也就是环的长度)
假设慢指针回到环的起点，设相遇点距环的起点距离为m，slow和fast再次相遇之后行走距离为k，，那么距头结点head的距离为k-m, 此时快指针距离相遇点也是k-m，因此慢指针回到节点之后两指针同速前进，k-m步就会相遇，相遇的地方就是环的起点了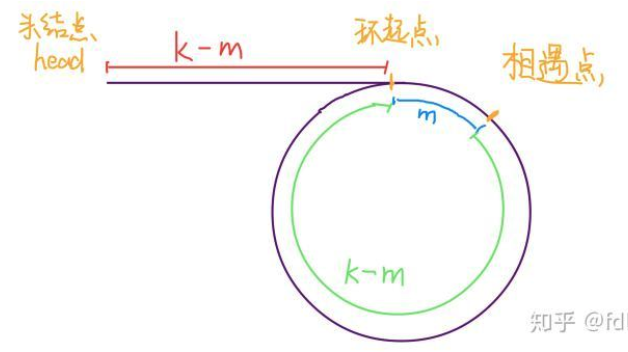
image.png

寻找链表的倒数K个元素

让快指针先走 k 步，然后快慢指针开始同速前进。这样当快指针走到链表末尾 null 时，慢指针所在的位置就是倒数第 k 个链表节点（为了简化，假设 k 不会超过链表长度）

1
2
3
4
5
6
7
8
9
ListNode slow, fast;
slow = fast = head;
while (k-- > 0) 
    fast = fast.next;
while (fast != null) {
    slow = slow.next;
    fast = fast.next;
}
return slow;

移除元素

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度

不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。

这里我们就可以使用快慢指针，在[0，slow)中的元素都是值不等于val=target的元素，fast指针用于扫描整个数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public int removeElement(int[] nums, int val) {
    // 慢指针slow 区间[0,slow)内的元素为值不等于val的元素
    int slow = 0;
    for(int fast = 0; fast < nums.length; fast++) {
        // 快指针fast所指向的元素值不等于val=3
        // 将其值赋值于慢指针所在位置
        if (nums[fast] != val) {
            nums[slow] = nums[fast];
            // 赋值完毕之后，慢指针右移一位，等待下一次赋值
            slow++;
        }
    }
    return slow;
}

左右指针

左右指针通常是使用两边索引值，一般初始化为 left = 0, right = nums.length - 1

二分查找

二分查找是经典的左右指针，(需要注意的细节是开闭区间),本题使用闭区间 [0,nums.length-1]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int binarySearch(int[] nums, int target) {
    int left = 0; 
    int right = nums.length - 1;
    if(nums[(left+right)/2] == target) return (left+right)/2;
    while(left <= right) {
        int mid = (right + left) / 2;
        if(nums[mid] == target)
            return mid; 
        else if (nums[mid] < target)
            left = mid + 1; 
        else if (nums[mid] > target)
            right = mid - 1;
    }
    return -1;
}

反转字数组(字符串)

字符串也是同理

1
2
3
4
5
6
7
8
9
10
11
void reverse(int[] nums) {
    int left = 0;
    int right = nums.length - 1;
    while (left < right) {
        // swap(nums[left], nums[right])
        int temp = nums[left];
        nums[left] = nums[right];
        nums[right] = temp;
        left++; right--;
    }
}

两数之和

image.png
通常通过hash法来解，这里是有序数组，因此也可以通过双指针来解决，类似二分查找变种，双指针处理有序数组还是很棒的，代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int[] twoSum(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left < right) {
        int sum = nums[left] + nums[right];
        if (sum == target) {
            // 题目要求的索引是从 1 开始的
            return new int[]{left + 1, right + 1};
        } else if (sum < target) {
            left++; // 让 sum 大一点
        } else if (sum > target) {
            right--; // 让 sum 小一点
        }
    }
    return new int[]{-1, -1};
}

滑动窗口

稍微复杂一点的双指针使用，核心就是维护一个窗口，调整窗口的大小，重点把握的是

  • 窗口内是什么
  • 窗口起始位置如何移动
  • 窗口结束位置如何移动

伪代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int left = 0, right = 0;

while (right < s.size()) {
    // 增大窗口
    window.add(s[right]);
    right++;
    //窗口数据更新……
    
    while (window needs shrink) {
        // 缩小窗口
        window.remove(s[left]);
        left++;
    }
}

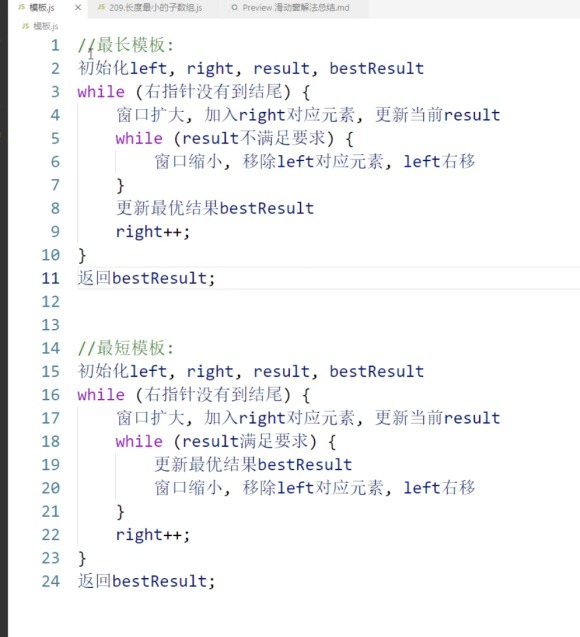
image.png

看个经典算法题

209.长度最小的子数组(mid)-滑动窗口
给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组，并返回其长度。如果不存在符合条件的子数组，返回 0，如:
输入：s = 7, nums = [2,3,1,2,4,3] 输出：2 解释：子数组 [4,3] 是该条件下的长度最小的子数组。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
//滑动窗口
fun minSubArrayLen(target: Int, nums: IntArray): Int {
    var sum = 0
    var subLength = 0
    var result = Int.MAX_VALUE

    //滑动窗口起始位置
    var left = 0

    for(right in nums.indices){
        //开始累加
        sum += nums[right]
        //滑动窗口
        while(sum >= target){
            subLength = right - left +1
            result = if(result < subLength) result else subLength
            //移动窗口左边界
            sum-=nums[left++]
        }
    }
    return if(result == Int.MAX_VALUE) 0 else result
}

关于滑动窗口 B站也有讲解视频 https://www.bilibili.com/video/BV1V44y1s7zJ?spm_id_from=333.1007.top_right_bar_window_history.content.click&vd_source=f9b305274daffa5db46d0a6df9e6bdfa